The Requirement for Background Radiation Compensation in Infrared Thermometry
Every warm or hot object emits infrared radiation. The radiated power P depends on the object’s core temperature T and its surface emissivity ε to The radiated power P is directly proportional to the object’s core temperature T and its surface emissivity ε as per the Stefan Boltzmann Law:
P∝ ε .T4
In its simplest form, infrared temperature measurement relies on measuring the emitted radiation from the object, knowing the surface emissivity, and performing a calculation to work out its temperature.
This is all well and good when the object is in the open air, and much hotter than its surroundings. As radiated power P increases with the 4th power of temperature in the equation above, hotter objects emit far more radiation. Thus pretty much all the radiation collected by the infrared thermometer will be coming from the object, and the simple calculation is valid.
The story is rather different for infrared temperature measurements inside a furnace, as in the example of Figure 1.

Fig. 1: Typical steel slab reheat furnace.
In this case the surroundings are hotter than the object by definition, as it is largely radiant energy from the walls and / or flames that is used to heat the object. An infrared thermometer pointed at the object will now be collecting both infrared radiation that the object emits itself, due to its own core temperature, and reflected radiation from the walls of the furnace. To correctly deduce the object temperature, this reflected component must be quantified and removed from the calculation.
The intensity of reflected radiation depends on the object surface emissivity in the opposite way to the intensity of core radiation. As all real objects have emissivity ε < 1 (ie. emissivity is always less than 100%) and most materials do not transmit any visible or infrared radiation, the reflectivity of the slab surface is given by γ= 1- ε.
For extremely shiny products such as bright metals, emissivity can be much lower than reflectivity. However even if emissivity is many times higher than reflectivity, reflected radiation can dominate the infrared signal from the object due to the T4 dependence of infrared radiation on temperature.
For example, consider a steel slab reheat furnace as shown in Figure 1. In a reheat furnace, a cold steel slab is heated to the desired temperature for further processing (eg. rolling) in a hot furnace environment.
Consider the arrangement shown in Figure 2. A pyrometer, line scanner or thermal imager detects the direct emitted radiation of the slab surface together with reflected radiation from the furnace refractory, which is (much) higher than the real object temperature.
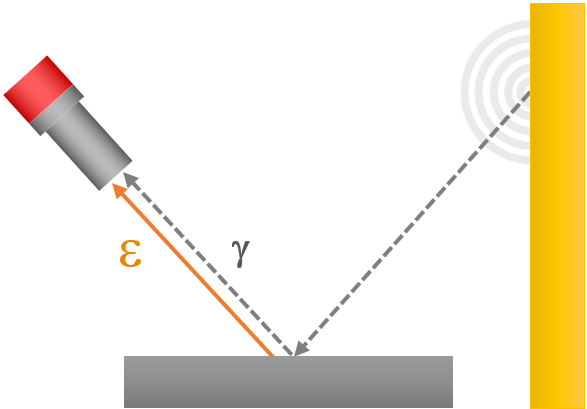
Fig. 2: Background reflection in a furnace.
Suppose the cool steel slab has a surface temperature of 100°C (373K) at the start of the heating process and the refractory furnace wall has a temperature of 1000°C (1273K). For a steel slab, emissivity is typically around 0.8 or 80% and reflectivity around 0.2 or 20%. The emissivity of the furnace wall will be close to 1 or 100% (more about this later).
The thermometer will receive infrared radiation P where
P∝ ε.T object 4+ γ.T wall 4
P∝ 0.8.373 4+ 0.2.12734
Simple calculation reveals that the contribution from the furnace wall is 34 times greater than that from the object itself.
Figure 3 shows the potential errors that can result from infrared temperature measurement without compensation for background radiation.
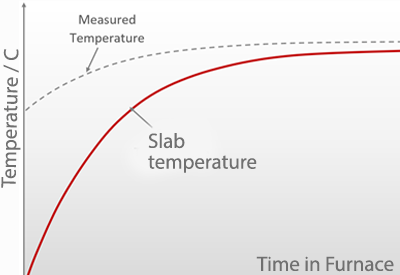
Fig. 3: Temperature values without compensation.
At the beginning of the heating process, when the furnace wall is so much hotter than the slab, the background radiation dominates the measurement. As the slab reaches thermal equilibrium, the influence of the background radiation becomes less significant, but it will still be present. To accurately track the temperature of the slab as it heats up, any infrared device must apply background compensation. Without background compensation, product temperatures would be measured too high, potentially leading to process and quality issues.
All AMETEK Land pyrometers, line-scanners, and thermal imaging systems provide a background compensation method. Various input methods allow input of a background temperature value – either a static value if the background temperature remains constant, or live input from a thermocouple or second background pyrometer measuring the furnace wall temperature as shown in Figure 4.
Fig. 4: Illustration of a reheat furnace application.

Fig. 4a: Pyrometer measurement without compensation.
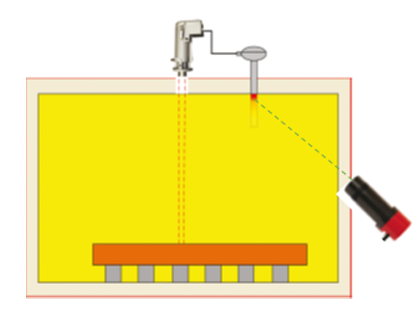
Figure 4b: Pyrometer measurement with compensation – either a surface thermocouple or a second pyrometer can be used to provide live background temperature measurement.
There are only two cases where background compensation is not necessary – when the background is so much cooler than the target to be measured that it contributes minimal signal, and when the background is at the same temperature as the target. The second case is the reason why the furnace wall has an effective emissivity value of 1. The refractory surface actually has emissivity less than 1, but the reduction in radiation from any point on the wall is exactly compensated for by reflected radiation from other areas of the furnace at roughly the same temperature.
In all other cases, live background compensation – and correct values for emissivity – are essential for accurate temperature reading in furnace environments.